The Gravity of the Situation
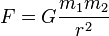
Gravitation
- F is the force between the masses;
- G is the gravitational constant (6.674×10−11 N · (m/kg)2);
- _m_1 is the first mass;
- _m_2 is the second mass;
- r is the distance between the centers of the masses.
For simplicity and performance reasons, there are a few things to be aware of though. Firstly, I decided not to worry about real world units since the planets, ships and torpedoes are not realistically scaled to each other (either by size, mass or distance from each other). This means I can decide that my torpedoes have a mass of 1, thereby eliminating a multiplication for the most common case. This also means I can choose the value of G to be whatever looks or feels right.
This is still quite a significant calculation that has to be performed every frame for every torpedo/planet pair.
As it turns out though, the maximum number of torpedo/planet pairs is quite low. Based on the limits of the previous version of Gravitas, there were at most 9 ships, firing at most 3 torpedoes, with at most 11 planets. This means 9 × 3 × 11 = 297 times to calculate the strength of the gravity each frame. In practice I don’t think I ever saw so that many torpedoes (every ship using a triple-shot special power at once).
But then I wanted to add dust. By dust, I mean a trail from the torpedoes, that is also affected by gravity. At a minimum this should generate one particle per frame and be at least a couple of seconds long at normal torpedo speed. This means each torpedo could easily have a hundred dust particles all needing the same gravity calculation. All of a sudden there could be 300,000 gravitation calculations per frame. On my laptop it ran fine. On my phone, not so much.
There are a number of possible ways of solving this issue, but the one I settled on is based on the principle that accuracy of simulation of the dust particles (as opposed to the torpedoes) is not so important. That is, if the dust particles don’t behave perfectly, it doesn’t really matter. One thing to notice about the gravity is that the only dynamic data it depends on is the position of the dust. The mass of the dust is fixed, and the position and mass of the planets are fixed (at least per round).
My solution was to pre-calculate the strength of gravity on a dust particle for all the positions in a low-resolution grid. This means I can “calculate” the gravity by doing a relatively cheap lookup.
